Modelling Agents As Vector Spheres

Agents are difficult to model due to the near-infinite variety of their states and transformations between states. A sphere has an infinite number of points on its surface. This property allows the compression of all relevant points onto the surface of a sphere.

In the simplest form of spherical agent modelling, agents are spheres with a vector between any two points representing their directionality. That is: the sum of an agent's models, goals, desires, etc. can be encoded as a vector through a sphere.

This model encodes a direction through the space of possibilities available to an agent. When modelled in this way, agents can effectively be regarded as particles that generate a gravitational field whose strength varies based on the length of the vector (which increases in length as an agent gains more data points and updates its models).
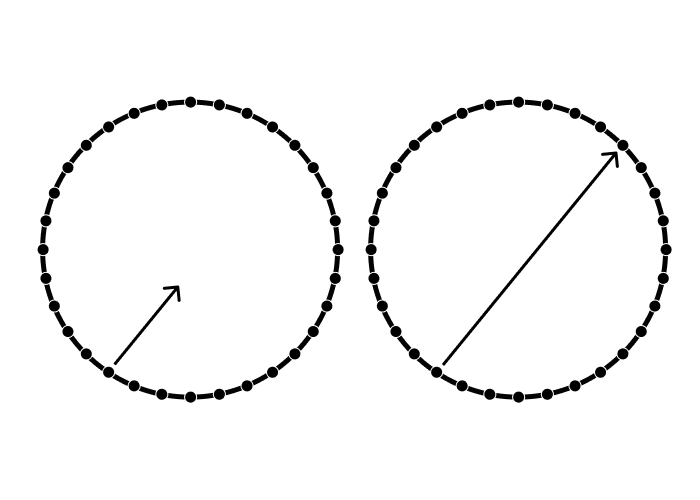
Agents with longer vectors have stronger fields. These agents influence other agents' vectors to drift in their direction, aligning multiple agents to the same directionality.
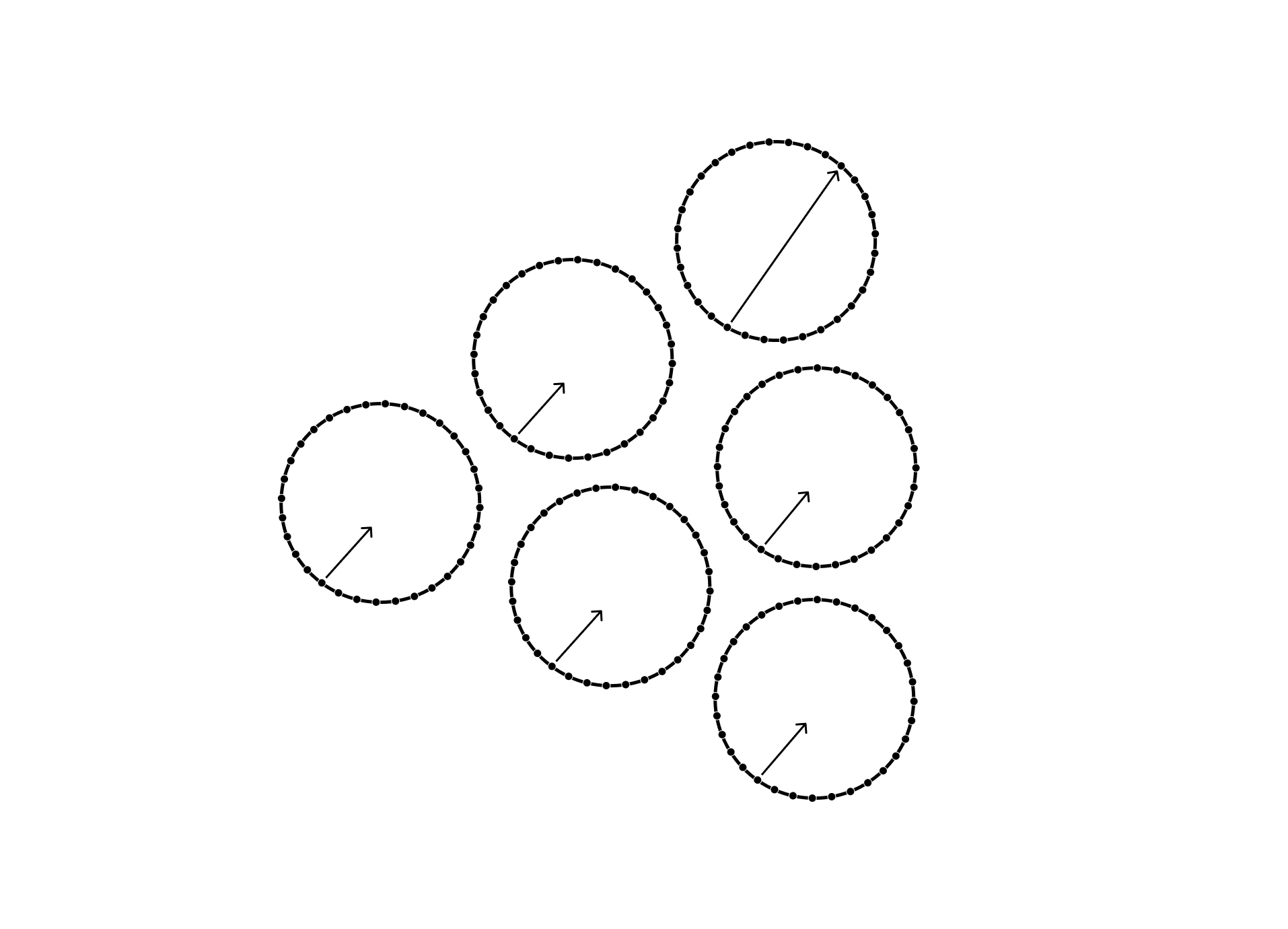
When multiple vectors of multiple directionalities and strengths interact, influence occurs depending on proximity and vector strength. For example, similarly strong vectors with relatively different directionality but close proximity will drift past each other with relatively little interference.
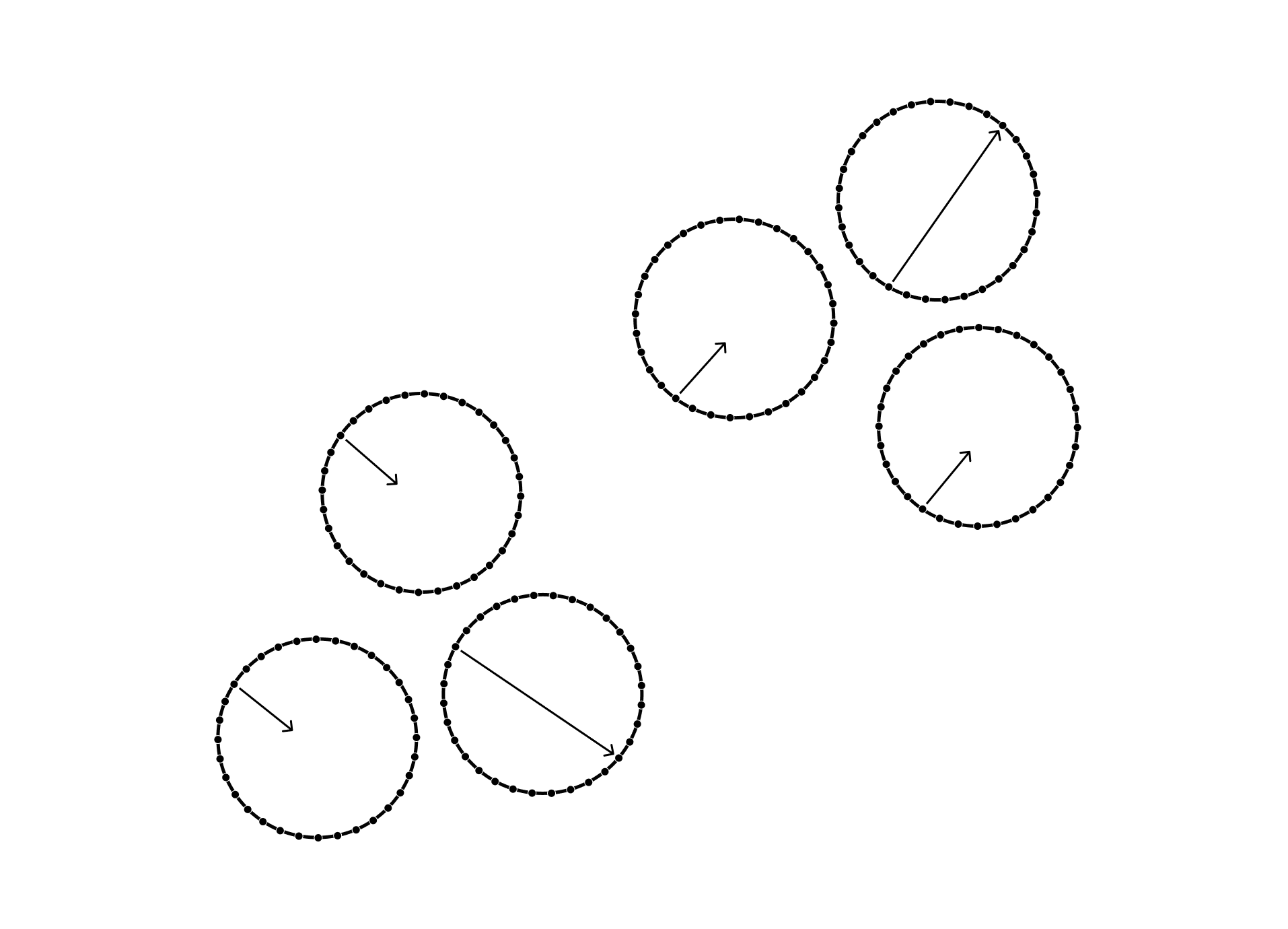
As more vectors align, their gravitational fields sum and form feedback loops that increase the vector strength of all agents with a similar enough directionality in range of their combined gravitational field.

The gravitational interactions of agents embedded in a possibility field enables the analysis of emergent behaviours from high-dimensional data sets. This type of analysis can theoretically generate a spherical vector that represents an entire system of agents and their directionality in possibility space.
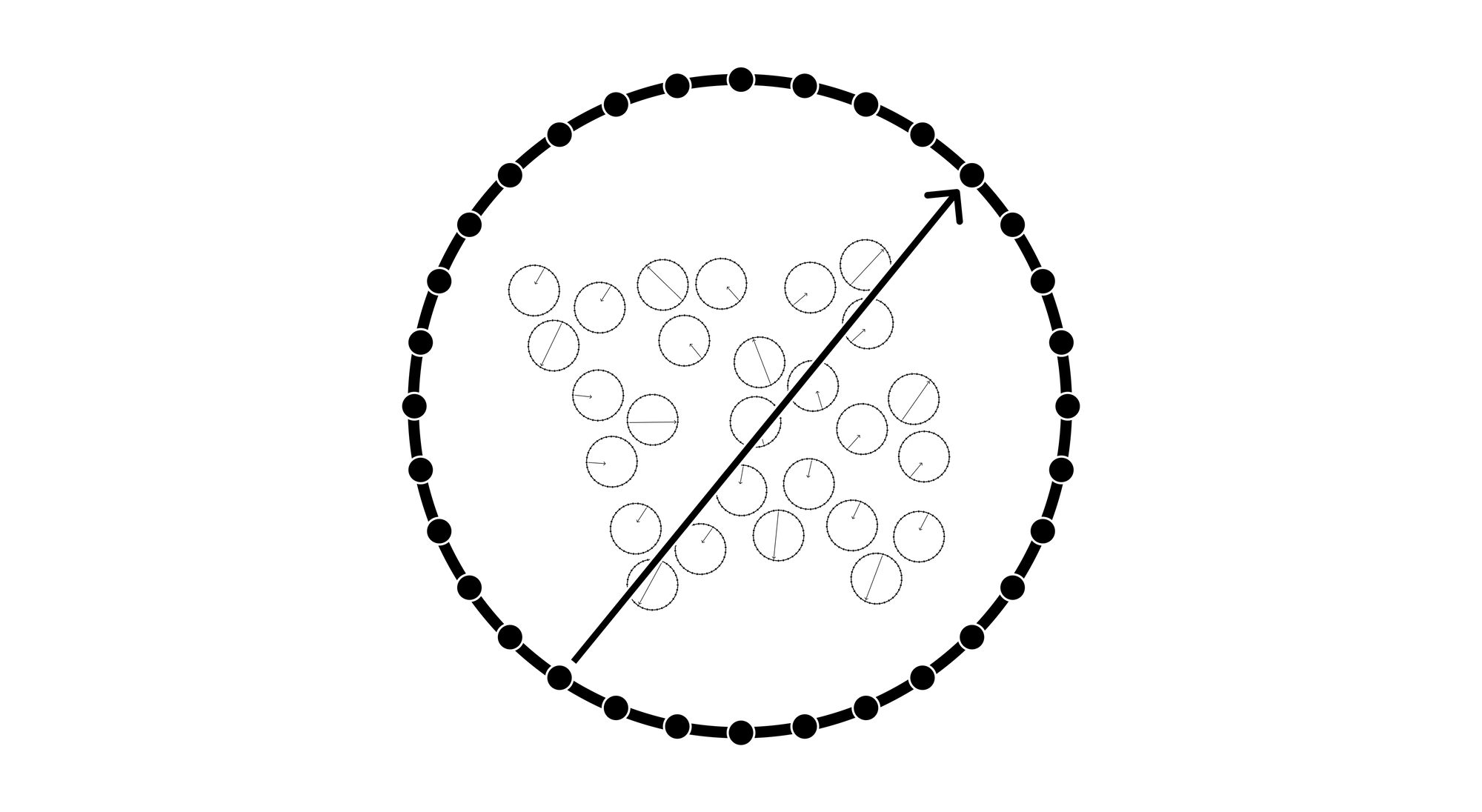
The self-similarity in this model enables us to use the same process by which we generate a global vector to model how agents are modelling each other, themselves, and the entire system. This means that the vector of an agent can also represent its theory-of-directionality for other agents and the global system in a way that's granular enough to zoom into and compare with the actual vectors of other agents and the global vector.

By computing the difference between the actual state of the system and the agents' models of the system and using that difference to determine the likelihood of different global vectors arising gives us a simple, robust model for prediction.
This model is in its infancy, but I have a strong feeling that it bears a close resemblance to the way that humans actually model others and make predictions.